Question

Kinda confused on this one an explanation would be very appreciated.It is p || q. I forgot to mark the lines the top one is "p" and the bottom one is "q".

Answer 1

You know that:

`x=12\degree`

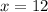
Notice that when the lines "p" and "q" are intersected by the transversal, one of the angles formed is represented with this expression:

`4x-2\mleft(6-3x\mright)`

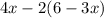
To find the measure of this angle, you need to substitute the value of "x" into the expression and then evaluate. You get that this is:

`\begin{gathered} =4(12\degree)-2\mleft(6-3(12\degree)\mright) \\ =48\degree-60\degree \\ =108\degree \end{gathered}`

By definition, when two parallel lines are intersected by a transversal, several pairs of angles are formed. One of these pairs is the pair of Exterior angles on the same of the transversal.

By definition, the Exterior angles on the same side of the transversal are Supplementary (they add up to 180 degrees) when the lines (intersected by the transversal) are parallel.

In this case, you can identify that:

`80\degree+108\degree=188\degree`

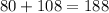
Therefore, you can determine that the angle that measures 80 degrees and the angle that measures 108 degrees are not Supplementary Angles.

Hence, the answer is: The lines "p" and "q" are not parallel.