Solution:
Given that;
An angle measures 3° more than two times its complement x.
Let the larger angle be y
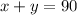
The angle measures 3° more than two times its complement, i.e.
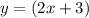
Then,
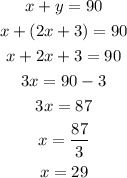
The smaller angle, x is 29 degrees
The larger angle is
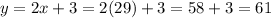
The larger angle, y is 61 degrees
The total is

The total is 90 degrees.