Question

Find the value V of the Riemann, using the partition P = {{0, 2}, {2, 5}, {5, 7}}

Answer 1

Before calculate the sum itself let's find the ck and the distance Δxk, we'll use the partition P = {{0,2}, {2,5}, {5,7}}, the problem says that the ck is the right endpoints of the partition, then

`\begin{gathered} \lbrack0,2\rbrack\Rightarrow c_1=2,\Delta x_1=2 \\ \lbrack2,5\rbrack\Rightarrow c_2=5,\Delta x_2=3 \\ \lbrack5,7\rbrack\Rightarrow c_3=7,\Delta x_3=2 \end{gathered}`

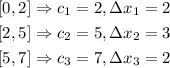
Now we have that we can write our Riemann sum

`\begin{gathered} V=\sum ^3_(k\mathop=1)f(c_k)\Delta x \\ V=f(c_1)\Delta x_1+f(c_2)\Delta x_3+f(c_3)\Delta x_3 \\ V=f(2)\cdot2+f(5)\cdot3+f(7)\cdot2 \\ V=2^2\cdot2+2^5\cdot3+2^7\cdot2 \\ V=360 \end{gathered}`

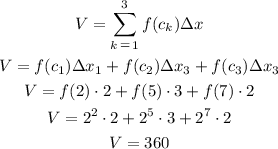
We can see, geometrically what we've done

We calculated the sum of the areas of the three green rectangles, if we do more partitions and some sums we will find that the sum will be the area under the graphic.