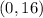Question

How would i be able to do the last bullet point?

Answer 1

So, we know some coordinates of the places:

- Home: (-3, -12)

- School: (-15, 6)

- Grocery: (24, 6)

- Gym: (0, y_gym)

First, we want to determine the line that represents a stree that connects School and Home, that is, the points (-15, 6) and (-3, -12).

Let's represent a line in the standard form:

`y=a+bx`

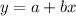
The slope, "b", can be calculated using the points we know:

`b=(y_2-y_1)/(x_2-x_1)=(6-(-12))/(-15-(-3))=(6+12)/(-15+3)=(18)/(-12)=-(3)/(2)`

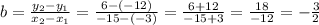
Then, we can use the slope-point form and solve for y:

`\begin{gathered} y-y_1=b(x-x_1) \\ y+12=-(3)/(2)(x+3) \\ y=-(3)/(2)x-(9)/(2)-12 \\ y=-(3)/(2)x-(33)/(2) \end{gathered}`

That is the equation of the First Street.

The Main Street passes through Home and Grocery, that is, points (-3 -12) and (24, 6).

Using the same method, we firts get the slope:

`b=(y_2-y_1)/(x_2-x_1)=(6-(-12))/(24-(-3))=(18)/(27)=(2)/(3)`

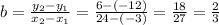
And use the slope-point form:

`\begin{gathered} y-y_1=b(x-x_1)_{} \\ y+12=(2)/(3)(x+3) \\ y=(2)/(3)x+2-12 \\ y=(2)/(3)x-10 \end{gathered}`

Lastly, we know that Ridge Road is parallel to Main Street and it passes through School. If they are parallel, they have the same slope, so the slope of Ridge Road is:

`b=(2)/(3)`

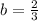
Since we know School is in thir Road, we can use the slope-point to get the equation for Ridge Road:

`\begin{gathered} y-y_1=b(x-x_1) \\ y-6=(2)/(3)(x+15) \\ y=(2)/(3)x+10+6 \\ y=(2)/(3)x+16 \end{gathered}`

And, since we know that the x-coordinate of the Gym is x = 0, we can put this into the equation of the Ridged Road to get its y-coordinate:

`\begin{gathered} y=(2)/(3)\cdot0+16 \\ y=16 \end{gathered}`

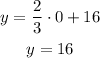
The picture we get is the following:

So, the final answers are:

First Street:

`y=-(3)/(2)x-(33)/(2)`

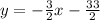
Main Street:

`y=(2)/(3)x-10`

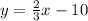
Ridge Road:

`y=(2)/(3)x+16`

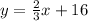
Coordinates of the Gym:

`(0,16)`