Find the least common multiple of these two monomials16xy^8 z ^5 \: and \: 20 {x}^(9) {y}^(4) {z}^(6)

Question

Find the least common multiple of these two monomials
`16xy^8 z ^5 \: and \: 20 {x}^(9) {y}^(4) {z}^(6)`

Answer 1

We are given two monomials

`16jk^8m^5`

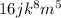
and

`20j^9k^4m^6`

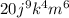
To find the lowest common multiple

we can express each of the monomials as follow

`16jk^8m^5=16* j* k^8* m^5`

`20* j^9* k^4* m^5`

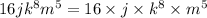
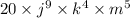
For the number part of the monomials,

The multiples of 16 are: 16, 32, 48, 64, 80, 96,-----

The multiples of 20 are : 20, 40, 60, 80, 100,-----

The lowest common multiple of 16 and 20 is 80

For the alphabet parts, the alphabet with the highest power

`\begin{gathered} \text{lowest common multiple of} \\ j\text{ and j}^9\text{ is j}^9 \\ k^4\text{ and }k^8\text{ is k}^8 \\ m^5\text{ and }m^6\text{ is m}^6 \end{gathered}`

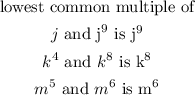
If we combine the terms to give the lowest common multiple, we will obtain

`80j^9k^8m^6`

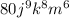
Thus, Option C is correct