The triangle has an angle of 90°, therefore it is a right triangle.
In this type of triangle, we can use the Pythagoras' theorem to find a relation between the smaller sides (legs) and the bigger side (hypotenuse).
If the result is false, the triangle is not a right triangle.
So testing each option, we have:
A)
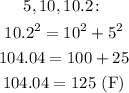
B)
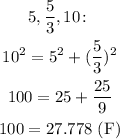
C)

D)

None of the options can represent a 30-60-90 triangle, unless the correct set of values for option B is: {5, 5√3, 10}. Then we would have:
![\begin{gathered} 5,5\sqrt[]{3},10\colon \\ 10^2=(5\sqrt[]{3})^2+5^2 \\ 100=25\cdot3+25 \\ 100=75+25 \\ 100=100\text{ (T)} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/dzpo7u91n2mdng34k09k8lt243170pqgz5.png)
So, in this case, the option would be B.