Question

Write the slope-intercept form of the equation of the line described. 7.) through: ( 2, 3 ) , perp to Y= -1/4x + 3

Answer 1

We need to find a linear equation of the form (slope-intercept form):

`y=mx+b`

Where, m is the slope of the equation, and b is the intercept (b is the value when x = 0).

We need to find an equation perpendicular to:

`y=-(1)/(4)x+3`

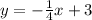
The perpendicular to this line must have a slope that is the inverse and reciprocal, then we have:

m1 = -1/4 ---> m2 = 4. That is, the product of both must be -1, that is:

`m_1\cdot m_2=-(1)/(4)\cdot4=-1`

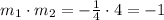
Therefore, we have the slope of m2 = 4. This equation passes through (2, 3). Using the Point-Slope Form of the line equation, we have:

`y-y_1=m(x-x_1)`

We have that x1 = 2, and y1 = 3. Then:

`y-3=4\cdot(x-2)\Rightarrow y-3=4x-8\Rightarrow y=4x-8+3\Rightarrow y=4x-5`

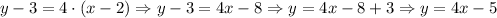
Thus, the slope-intercept form of the line that passes through the coordinates ( 2, 3), and is perpendicular to y= -1/4x + 3 is y = 4x - 5.

We can see these two lines ( the blue one is y = 4x - 5). See that passes through (2, 3).

They are perpendicular.