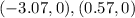
Step-by-step explanation
Step 1
given the function:
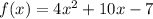
we know that the x-intercept is the x-coordinate of a point where the parabola intersects the x-axis, this happens when y =0
so, we need to set the function equals zero and solve for x
a) use the quadratic formula
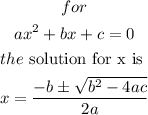
so
let
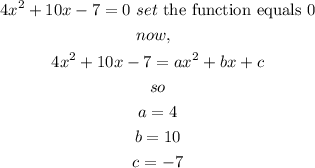
now, replace in the quadratic formula
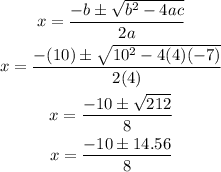
therefore,
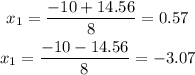
so, the coordinates are:
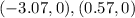
I hope this helps you
.