Question

Find the type and number of roots of the following equations using the discriminantQuestion 1

Answer 1

Given the question in the image, the following are the solution steps to answer the question.

STEP 1: Write the quadratic equation

`x^2-8x+16=0`

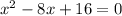
STEP 2: Define how to use discriminant to find the nature of the roots of a quadratic equation

To determine the nature of roots of quadratic equations (in the form ax^2 + bx +c=0) , we need to caclulate the discriminant, which is b^2 - 4ac.

When discriminant is greater than zero, the roots are unequal and real.

When discriminant is less than zero, the roots are imaginary.

STEP 3: Compare with the standard quadratic equation to get the needed parameters

`\begin{gathered} ax^2+bx+c=0---\text{ Standard quadratic equation} \\ x^2-8x+16=0 \\ By\text{ comparison;} \\ a=1,b=-8,c=16 \end{gathered}`

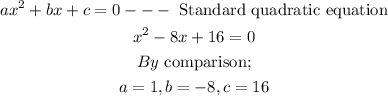
STEP 4: Calculate the discriminant of the equation

`\begin{gathered} d=b^2-4ac \\ By\text{ substitution}, \\ d=(-8^2_{})-4(1)(16) \\ d=64-64=0 \\ \text{Discriminant}=0 \end{gathered}`

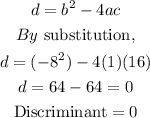
Since the discriminant of the quadratic equation is equal to zero and using the explanation given in step 2 above. Hence, there is exactly one root for the equation and it is a real root.