Question

A toy boat is seen floating down a river. The toy boat is first spotted 60 feet away. A few moments later the toy boat is 45 feet away, making a 55° angle between thetwo sightings. How far did the toy boat travel? Round to the nearest tenth.

Answer 1

Step 1:

In this question, we are given the following:

A toy boat is seen floating down a river.

The toy boat is first spotted 60 feet away.

A few moments later the toy boat is 45 feet away, making a 55° angle between the two sightings.

How far did the toy boat travel? Round to the nearest tenth.

Step 2:

The details of the solution are as follows:

The details of the diagram are as follows



Using cosine rule

`c^2=a^2+b^2-2(a)(b)\cos (C)`

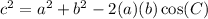
Here

`\begin{gathered} a=60ft \\ b=45ft \\ C=55^0 \end{gathered}`

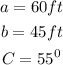
`\begin{gathered} c^2=60^2+45^2-2(60)(45)\cos (55^0) \\ \\ \Rightarrow c=\sqrt[]{60^2+45^2-2(60)(45)\cos(55^0)}=\sqrt[]{2527.687244}\approx50.3(\text{ to the nearest tenth}) \end{gathered}`

Conclusion

Therefore, the toy boat traveled a distance of 50.3 feet (