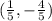A point C between two other points A and B, in the line joining A to B, is a linear combination of A and B.
If C is a/n the distance from B to A, then it is (n-a)/n the distance from A to B. We can write that as:
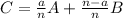
Notice that the farther it is from B (as a increases), the larger is the factor (a/n) by which we multiply A.
Step 1
Identify the points A and B, and the fractions a/n and (n-a)/n.
We have:
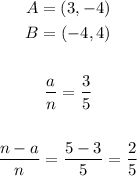
Step 2
Use the previous result in the formula to find C:
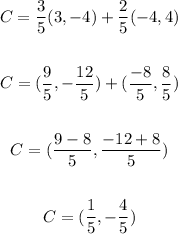
Answer
Therefore, the point that is 3/5 the distance from B to A is