Answer:
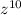
Explanation:
Given the expression below:
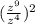
Step 1: Apply the division law of indices.
If we have the same base, and the expression is being divided, subtract the indices.
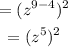
Step 2: Multiply the indices by the index law of powers.
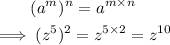
The simplified expression is z^(10).