Question

What is the sum of the arithmetic series? 17 + 22 + 27 + 32 + 37 + ... + 67395445462202

Answer 1

Determine the common difference for the sequence.

`\begin{gathered} d=22-17 \\ =5 \end{gathered}`

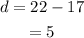
The first term of sequanece is a = 17.

Determine the number of terms in the sequence.

`\begin{gathered} 67=17+(n-1)\cdot5 \\ (n-1)=(50)/(5) \\ n=10+1 \\ =11 \end{gathered}`

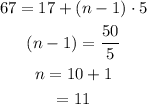
The formula for the sum of n terms of airthmetic sequence is,

`S=(n)/(2)\lbrack2a+(n-1)d\rbrack`

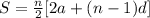
Substitute the values in the formula to determine the sum of airthmetic sequence.

`\begin{gathered} S=(11)/(2)\lbrack2\cdot17+(11-1)\cdot5\rbrack \\ =(11)/(2)\lbrack34+50\rbrack \\ =(11)/(2)\cdot84 \\ =11\cdot42 \\ =462 \end{gathered}`

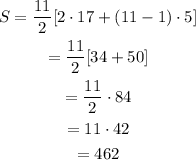
Thus sum of aithmetic series is 462.