Use integration by substitution to solve the integral below. Use C for the constant of integration.

Question

asked Feb 28, 2023 9.7k views

1 Answer

Billy Baker · Answer 1 · 2023-03-07T17:07:55+0000

SOLUTION

Write out ythe expression

Let

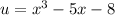
Differrentiate u with respect to x

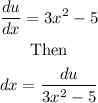
$\begin{gathered} (du)/(dx)=3x^2-5 \\ \text{Then} \\ dx=(du)/(3x^2-5) \end{gathered}$

Then, substitute into the expression above

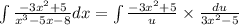
$\int (-3x^2+5)/(x^3-5x-8)dx=\int (-3x^2+5)/(u)*(du)/(3x^2-5)$

Then

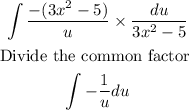
$\begin{gathered} \int (-(3x^2-5))/(u)*(du)/(3x^2-5) \\ \text{Divide the common factor } \\ \int -(1)/(u)du \end{gathered}$

Apply the rule

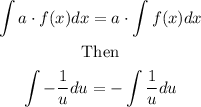
$\begin{gathered} \int a\cdot f\mleft(x\mright)dx=a\cdot\int f\mleft(x\mright)dx \\ \text{Then} \\ \int -(1)/(u)du=-\int (1)/(u)du \end{gathered}$

Then use the common integral rule

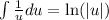
$\int (1)/(u)du=\ln \mleft(\mleft|u\mright|\mright)$

Replace the expression for u, we have

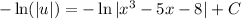
$-\ln (|u|)=-\ln \mleft|x^3-5x-8\mright|+C$

Therefore

The solution becomes

- ln |x³-5x - 8 | +C