Question

Solve the following system of equations using the Substitution Method. Use the infinity symbol if infinitelymany solutions exist, or enter DNE for no solutions. X-6y=-29 and -x-7y=-23

Answer 1

`\begin{gathered} x=-5 \\ y=4 \end{gathered}`

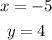
Step-by-step explanation

`\begin{gathered} x-6y=-29\rightarrow equation(1) \\ -x-7y=-23\rightarrow equation(2) \end{gathered}`

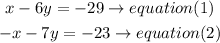
Step 1

a) isolate the x value in equatino (1) and substitute teh value in equation (2)

`\begin{gathered} x-6y=-29\rightarrow equation(1) \\ \text{add 6y in both sides} \\ x-6y+6y=-29+6y \\ x=6y-29 \end{gathered}`

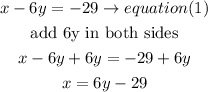
now, substitute in equation (2) and solve for y

`\begin{gathered} -x-7y=-23\rightarrow equation(2) \\ -(6y-29)-7y=-23 \\ -6y+29-7y=-23 \\ -13y+29=-23 \\ \text{subtract 29 in both sides } \\ -13y+29-29=-23-29 \\ -13y=-52 \\ \text{divide both sides by -13} \\ (-13y)/(-13)=(-52)/(-13) \\ y=4 \end{gathered}`

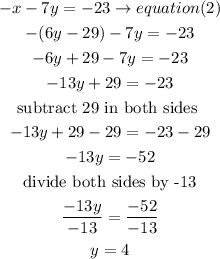
Step 2

now,replace the y value in equation 1 and solve for x

`\begin{gathered} x-6y=-29\rightarrow equation(1) \\ \text{replace} \\ x-6(4)=-29 \\ x-24=-29 \\ add\text{ 24 in both sides} \\ x-24+24=-29+24 \\ x=-5 \end{gathered}`

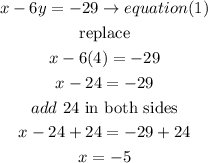
so

x=-5

therefore, the system has one solution

`\begin{gathered} x=-5 \\ y=4 \end{gathered}`

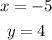
I hope this helps you