Question

A company has two warehouses that are 360 miles apart. A truck leaves Warehouse A and heads towards Warehouse B traveling at 45 miles per hour. At the same time, a truck leaves Warehouse B and heads towards Warehouse A traveling at 60 miles per hour. How long will the trucks be driving before they meet each other on the road?

between 1 and 2 hours
between 2 and 3 hours
between 3 and 4 hours
between 4 and 5 hours

Answer 1

Between 3 and 4 hours

Explanation:

Let's turn the sentence into an equation, suppose that both trucks will be traveling at a constant rate, let x be the number of hours truck A has been traveling, and let y be the number of hours truck B has been traveling. Then we can set up the equation:

`45x+60y=360`

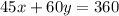
Both of these terms must add up to 360 since that will be the point where both trucks will meet. To solve this, we can use a graphing calculator:

(see picture)

Since both trucks left the warehouses at the same time, we need that:
`x=y`

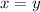
And the point in the graph that x=y is around 3.42 and 3.44, so we can conclude that both trucks must be traveling for 3-4 hours for them to meet on the road.

I hope this helps.