Question

An electron is accelerated by a potential difference of 702.06 kV. How fast is the electron moving if it started from rest?

Answer 1

Find the kinetic energy of the electron after moving through the potential difference of 702.06kV.

The electric potential energy of a charge is transformed in kinetic energy when it passes through a potential difference V. Then, the kinetic energy of the electron is:

`K=e\cdot V`

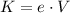
Where e is the charge of an electron:

`e=1.602*10^(-19)C`

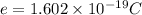
On the other hand, the kinetic energy of a particle with mass m is related to its speed:

`(1)/(2)mv^2=K`

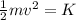
In this case, m is the mass of the electron:

`m=9.11*10^(-31)kg`

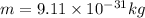
Then:

`(1)/(2)mv^2=eV`

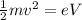
Isolate the speed v from the equation:

`v=\sqrt{(2eV)/(m)}`

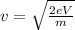
Replace the values for e, m and V=702.06kV to find the speed of the electron:

`v=\sqrt{(2(1.602*10^(-19)C)(702.06*10^3V))/(9.11*10^(-31)kg)}=4.969*10^8(m)/(s)`

Notice that the speed of the electron calculated using the classical method is greater than the speed of light:

`c=3*10^8(m)/(s)`

Then, the theory of Special Relativity is required to find a proper answer for this problem.

Therefore, the (inadequate) answer is: the electron is moving at a speed of approximately 4.97*10^8m/s according to Classical Physics.