In this problem, we want to apply the use of a quadratic function.
We are given the following equation to model the path of a rocket:
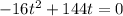
To find how long it takes the rocket to hit the ground, the equation must be equal to 0. Luckily, that's already true.
Begin by identifying the greatest common factor of
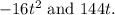
We see that both terms have 16 and t in common:

We can factor that expression out from each term to get:
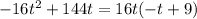
Now we have the equation:

Applying the zero product property, we can split this into two equations:
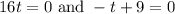
Solve the first equation by dividing by 16 on both sides:
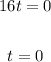
Solve the second equation by adding t to both sides:
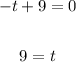
Since we want to know how long it takes the rocket to hit the ground after takeoff, we can ignore the first solution, which represents 0 seconds.
It took the rocket 9 seconds to hit the ground.