ANSWER
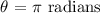
Step-by-step explanation
We are given that the radius of the circle is 3 inches and the length of the arc that subtends the angle is 3π inches.
We can find the angle subtended by the arc by using the formula for length of an arc:
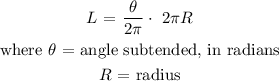
Therefore, we have that:
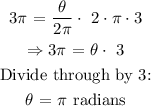
That is the angle subtended by the arc.