Question

A vibrating string has a frequency of 200 Hz. What will its frequency be if:A. Its length is decreased to ¼ of its original length?B. Its tension is quadrupled?

Answer 1

Given data:

* The frequency of the string vibration is f = 200 Hz.

Solution:

(A). The frequency of vibration in terms of the length of the string is,

`f=\frac{\sqrt[]{T}}{L}`

If the length of the string is decreased to 1/4 of its actual value, then the frequency of the string is,

`\begin{gathered} f^(\prime)=\frac{\sqrt[]{T}}{(L)/(4)} \\ f^(\prime)=\frac{4\sqrt[]{T}}{L} \\ f^(\prime)=4f \end{gathered}`

Substituting the known values,

`\begin{gathered} f^(\prime)=4*200\text{ } \\ f^(\prime)=800\text{ Hz} \end{gathered}`

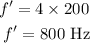
Thus, the frequency of the vibration in the given case is 800 Hz.

(B). If the tension of the string is quadrupled, that is its value becomes 4 times the actual value, then the frequency of the vibration is,

`\begin{gathered} f^(\prime)=\frac{\sqrt[]{4T}}{L} \\ f^(\prime)=\frac{2\sqrt[]{T}}{L} \\ f^(\prime)=2f \end{gathered}`

Substituting the known values,

`\begin{gathered} f^(\prime)=2*200 \\ f^(\prime)=400\text{ Hz} \end{gathered}`

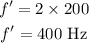
Thus, the frequency of the vibration becomes 400 Hz.