Question

Prove the following statements by contradiction (or directly, if you can or prefer)

Answer 1

we know that

The difference between a rational number and n irrational number is always an irrational number

Example

`\begin{gathered} 2-\sqrt{2\text{ }}\text{ = irrational number} \\ 2-e=irrational\text{ number} \\ \end{gathered}`

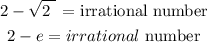
Prove by contradiction

The difference between a rational number and an irrational number is a rational number

we have that

`2-√(2)=is\text{ not a rational number}`

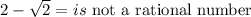
therefore

By contradiction, the original statement is true