Question

In FIGURE 3 a 1400 kg granite block is pulled up an incline plane at a constant speed of 1.34 m/s by a cable and winch. The indicated distances are d1 = 40 m and d2 = 30 m. The coefficient of kinetic friction between the block and the incline is 0.40. What is the power ofthe cable's force applied to the block?

Answer 1

Given:

The mass of the granite block is: m = 1400 kg

The granite block moves with the constant speed of: v = 1.34 m/s

The distance d1 is: d1 = 40 m

The distance d2 is: d2 = 30 m

The coefficient of kinetic friction of the block and the incline is: μ = 0.40

To find:

The power of the cable's force applied to the block.

Step-by-step explanation:

The forces acting on the block can be resolved into its components as:

The tension in the rope is given as:

`T=mgsinθ+f`

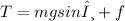
Here, f is the force of friction, which is given as:

`f=\mu N`

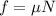
The normal force is balanced by the mgcosθ, thus,

`N=mgcosθ`

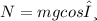
Thus, the tension in the string is given as:

`T=mgsinθ+\mu mgcosθ`

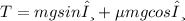
The angle θ made by inclined with the horizontal can be calculated as:

`\begin{gathered} θ=tan^(-1)(\frac{30\text{ m}}{40\text{ m}}) \\ \\ θ=tan^(-1)(0.75) \\ \\ θ=36.87\degree \end{gathered}`

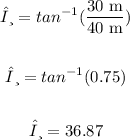
The tension in the string can be calculated as:

`\begin{gathered} T=1400\text{ kg}*9.8\text{ m/s}^2* sin(36.87\degree)+0.40*1400\text{ kg}*9.8\text{ m/s}^2* cos(36.87\degree) \\ \\ T=12622.41\text{ kg.m/s}^2 \end{gathered}`

Now the power P of the cable's force applied to the block can be calculated as:

`P=Tv`

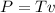
Substituting the values in the above equation, we get:

`\begin{gathered} P=12622.41\text{ kg.m/s}^2*1.34\text{ m/s} \\ \\ P=16914.03\text{ kg.m}^2\text{/s}^3 \\ \\ P=16914.03\text{ J/s} \\ \\ P=16914.03\text{ W} \end{gathered}`

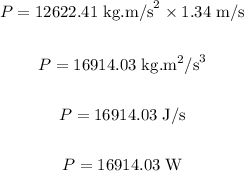
Final answer:

The power of the cable's force applied to the box is 16914.03 W.