Question

two circles are similar. If the larger circle has an area that is 225 times larger than the small circle, how many times bigger is its radius?

Answer 1

Case: Areas

Metho:

The larger circle has an area that is 225 times larger than the small circle.

Let the large area be 'A' and the radius is R

AND thesmaller area be a'' and radius is Rr

`(A)/(a)=225`

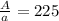
Applying the formula for Area of the similar circles

`\begin{gathered} (A)/(a)=225 \\ (\pi R^2)/(\pi r^2)=225 \\ (R^2)/(r^2)=225 \\ Take\text{ }the\text{ }square-root\text{ } \\ \sqrt{(R^2)/(r^2)}=√(225) \\ (R)/(r)=15 \\ R=15r \end{gathered}`

Final answers:

From the above, the bigger circle has a rdius i5 times tehe smaller one