To answer this question we will use the Pythagorean theorem.
Let l be the length (in meters) of the longer leg, then the length of the shorter (in meters) leg will be l-1.
Using the Pythagorean theorem we get:
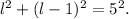
Simplifying the above result we get:
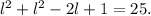
Adding like terms we get:
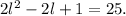
Subtracting 25 from the above equation we get:
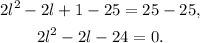
Dividing the above equation by 2 we get:
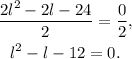
Now, notice that:
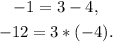
Then:
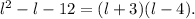
Therefore:
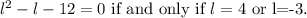
Since l is the length of a leg of a right triangle, then l>0, therefore l=4.
Answer:
Length of the shorter leg: 4m.
Length of the longer leg: 3m.
Length of the hypotenuse: 5m.