Question

A computer program found that the line c = 2t - 89 is a good fit for the data, Use this equation to predict how many cups of lemonade Lin might sell on a day when the high temperature is 74 degrees. Enter your answer in the box below. Answer:Ocups. The high temperature this Sunday is expected to be 5 degrees warmer than the high temperature this Saturday. Using the line c = 2t - 89. how many more cups of lemonade should Lin expect to sell on Sunday than Saturday? Explain or show your reasoning. Enter your response here

Answer 1

Part 1. Find how many cups will Lin sell when the high temperature is 74°.

We are given the expression:

`c=2t-89`

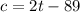
Where is c is the number of cups that Lin might sell and t is the high temperature.

We have the value of the high temperature:

`t=74`

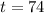
And to solve this problem we need to substitute t=74 into the given expression:

`\begin{gathered} c=2t-89 \\ \text{Substituting t=74} \\ c=2(74)-89 \end{gathered}`

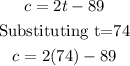
Solving the operations:

`\begin{gathered} c=148-89 \\ c=59 \end{gathered}`

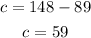
Answer (for part 1): 59 cups.

Part 2. Find how many more cups of lemonade Lin should sell on Sunday than Saturday.

We will call the high temperature on Saturday "x". The number of cups that Lin Might sell for x temperature is:

`c=2x-89`

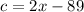
Now, we are told that the temperature on Sunday is expected to be 5° warmer, so we represent the high temperature on Sunday as 5 more than the temperature on Saturday (which we called x).

Thus, the temperature on Sunday is:

`t=x+5`

And we substitute this into the expression:

`\begin{gathered} c=2t-89 \\ \text{Substituting t=x+5} \\ c=2(x+5)-89 \end{gathered}`

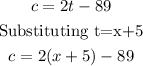
Using the distributive property on the right-hand side of the equation:

`\begin{gathered} c=2x+2\cdot5-89 \\ c=2x+10-89 \end{gathered}`

Re-arranging the expression:

`c=(2x-89)+10`

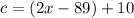
Comparing this with the expression we got for Saturday:

`\begin{gathered} \text{Saturday:} \\ c=2x-89 \\ \text{Sunday:} \\ c=(2x-89)+10 \end{gathered}`

As you can see, 10 more cups were sold on Sunday than on Saturday.

Answer (for part 2): 10 more cups