Given:
The objective is to find f(-4).
Step-by-step explanation:
The general equation of a straight line is,
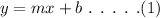
Here, m represents the slope of the straight line, b represents the y-intercept.
To find m:
The value of slope can be calculated by considering two coordinates from the graph,
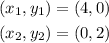
On plugging the values in the formula of the slope,
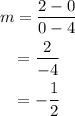
Thus, the slope of the graph is -1/2.
From the graph, the y-intercept of the graph is 2.
On plugging the obtained values in equation (1),
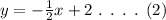
At x = -4 in equation (2),
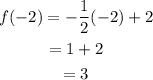
Hence, the value of f(-4) is 3.