We are asked to graph the following parabola
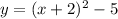
Let us compare this equation with the standard vertex form.
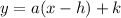
The vertex is the point (h, k)
So, the vertex of the given equation is (-2, -5)
Now let us find the y-intercept.
Substitute x = 0 into the given equation

So, the y-intercept point is (0, -1)
Now let us find the x-intercepts.
Substitute y = 0 into the given equation
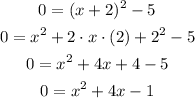
Use the quadratic formula to solve the above quadratic equation

Where a = 1, b = 4 and c = -1
![\begin{gathered} x=\frac{-4\pm\sqrt[]{4^2-4(1)(-1)}}{2(1)} \\ x=\frac{-4\pm\sqrt[]{16^{}+4}}{2} \\ x=\frac{-4\pm\sqrt[]{20}}{2} \\ x=\frac{-4+\sqrt[]{20}}{2},x=\frac{-4-\sqrt[]{20}}{2} \\ x=0.236,\: x=-4.236 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/h8is7ng399o6pe7xtov79bu7derh0c784p.png)
So, the x-intercepts are (0.236, 0) and (-4.236, 0)
Now let us plot all these points and sketch the graph of the parabola