Question

Help in example number two in the bottom right corner f(x) = -2x^2 - 8x + 1

Answer 1

`\begin{gathered} \text{Given} \\ f(x)=-2x^2-8x+1 \end{gathered}`

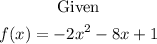
First, find the vertex of the given function, we have

`\begin{gathered} f(x)=-2x^2-8x+1 \\ \\ \text{The coefficients are } \\ a=-2,b=-8,c=1 \\ \\ \text{The x-coordinate of the vertex is at } \\ x=-(b)/(2a) \\ x=-(-8)/(2(-2)) \\ x=-(-8)/(-4) \\ x=-2 \end{gathered}`

Next, substitute x = -2. to the given function and we get

`\begin{gathered} f(x)=-2x^(2)-8x+1 \\ f(-2)=-2(-2)^2-8(-2)+1 \\ f(-2)=-2(4)+16+1 \\ f(-2)=-8+17 \\ f(-2)=9 \end{gathered}`

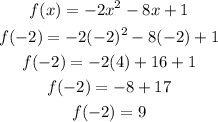
Therefore, the vertex is at (-2.9).

The axis of symmetry is at x = -2.

The y-intercept at y = 1.

The x-intercepts are the following:

`\begin{gathered} x=( -b \pm√(b^2 - 4ac))/( 2a ) \\ x = ( -(-8) \pm √((-8)^2 - 4(-2)(1)))/( 2(-2) ) \\ x=(8\pm√(64-(-8)))/(-4) \\ x = ( 8 \pm √(72))/( -4 ) \\ x = ( 8 \pm 6√(2)\, )/( -4 ) \\ \text{ Which becomes} \\ \\ x=(8+6√(2)\,)/(-4)\approx−4.12132 \\ x=(8-6√(2)\,)/(-4)\approx0.12132 \end{gathered}`

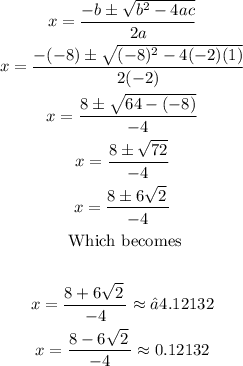
Graphing the function we get