Question

Solve the equation 2x2 - x - 5 = 1 using the quadratic formula.

Answer 1

For a general quadratic polynomial of the form:

`ax^2+bx+c=0`

the solution is

`x_(1,2)=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

this formula is called "the quadratic formula". There are 2 solutions indicated by the subindex 1 and 2 in x.

In our case, by comparing polynomials, we can see that

`\begin{gathered} a=2 \\ b=-1 \\ c=-6 \end{gathered}`

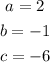
becuase our polynomial is

`2x^2-x-6=0`

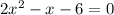
in which we moved 1 to the left hand side as -1.

Then, by applying the quadratic formula, we have

`x_(1,2)=\frac{-(-1)\pm\sqrt[]{(-1)^2-4(2)(-6)}}{2(2)}`

Then ,the first solution is

`x_1=\frac{-(-1)+\sqrt[]{(-1)^2-4(2)(-6)}}{2(2)}`

and the