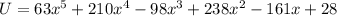Question

a/ Find a polynomial U with integer coefficientsthat satisfies the given conditions: degree 5, theleading coefficient 63, and zeros are 1/3, whichhas multiplicity 2, -4, and i

Answer 1

Since the zeroes are 1/3 which has multiplicity 2, -4 and i, then

The factors of the polynomial are

`x=(1)/(3)\rightarrow3x=1\rightarrow(3x-1)\rightarrow(3x-1)^2`
`x=-4\rightarrow(x+4)`
`x=i\rightarrow(x-i)(x+i)\rightarrow x^2-i^2\rightarrow(x^2+1)`

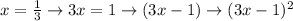
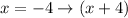
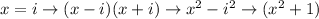
Multiply the 3 factors

`\begin{gathered} (3x-1)^2=(9x^2-6x+1) \\ U=(9x^2-6x+1)(x+4)(x^2+1) \end{gathered}`

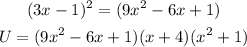
Multiply The first 2 brackets

`U=(9x^3+36x^2-6x^2-24x+x+4)(x^2+1)`

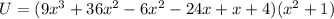
Add the like terms in the 1st bracket

`U=(9x^3+30x^2-23x+4)(x^2+1)`

Multiply the 2 brackets

`U=9x^5+30x^4-23x^3+4x^2+9x^3+30x^2-23x+4`

Add the like terms

`U=9x^5+30x^4-14x^3+34x^2-23x+4`

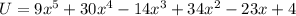
Since the leading coefficient is 63, multiply all terms by 7

`U=63x^5+210x^4-98x^3+238x^2-161x+28`