Question

Order the sides of the triangle from shortest to longest. (HINT: You need to find the missing angle first!) 85 40° X V

Answer 1

To find the missing angle we use that the sum of the inner angles of a triangle must add up 180º:

`\angle W+\angle V+\angle X=180º`

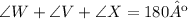
We know W and V, so we clear X:

`\angle X=180º-\angle W-\angle V=180º-80º-40º=60º`

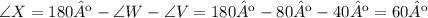
To order the sides, you don't need the size of them. Let's take a look at the angles:

So, since the angle with vertex on W is the widest, the opposite side to it (the segment XV) will be the longest. Then, the second angle is the one in X, so the second largest side will be it's opposite side (segment WV).

And finally but not last, the shortest side will be the oposite one to the narrowest angle, the one in V.

In summary, the sides ordered from shortest to longest are: c-a-b