Question

Jim has a total of 77 red and Blue marbles. The number of blue marbles is five more than twice the number of red marbles.A. Write a pair of linear equations to represent the information. Be sure to state what the variables represent.B. Explain the substitution method of solving this pair of equations. Solve the equations to find the number of red marbles.

Answer 1

A.

Jim has a total of red and blue marbles.

Let "r" represent the number of red marbles and "b" represent the number of blue marbles, to determine the total number of marbles he has, you have to add both, so that:

`r+b=77`

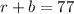
You know that the number of blue marbles "b" is five more than twice the number of red marbles "r"

Twice the number of red marbles means that r is multiplied by 2, you can express it as "2r", and he has five more than twice the number of red marbles, then you have to add 5 to 2r. You can express the number of blue marbles as follows:

`b=2r+5`

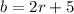
B.

Using both equations you can calculate the values of b and r using the substitution method.

We know that b=2r+5, and that r+b=77, the substitution method allows us to replace the known value of b, which is "2r+5" into the equation "r+b=77", this way we will determine one equation with only one variable "r":

`\begin{gathered} r+b=77\to\text{if b=2r+5} \\ r+(2r+5)=77 \end{gathered}`

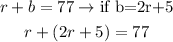
From this expression, you can determine the value of r, first erase the parentheses, and simplify the like terms:

`\begin{gathered} r+2r+5=77 \\ 3r+5=77 \end{gathered}`

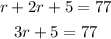
Second, pass 5 to the other side of the expression by applying the opposite operation to both sides of the equal sign:

`\begin{gathered} 3r+5-5=77-5 \\ 3r=72 \end{gathered}`

Third, divide both sides by 3 to reach the value of r:

`\begin{gathered} (3r)/(3)=(72)/(3) \\ r=24 \end{gathered}`

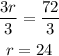
He has 24 red marbles