Question

According to the Rational Root Theorem, which of the following could be a root of p(x)=3x3−5x2+4? Select all that apply.

Answer 1

The rational root theorem, also called rational root test theorem state that for a polynomial equation in one variable with integer coefficients to have a solution (root) that is a rational number, the leading coefficient (the coefficient of the highest power) must be divisible by the denominator of the fraction and the constant term (the one without a variable) must be divisible by the numerator.

Given the polynomial

`p(x)=3x^3-5x^2+4`
`\begin{gathered} \text{Leading co}eficient\text{ =3} \\ \text{Constant term =4} \end{gathered}`

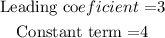
The factor of the constant term is

`\pm1,\pm2,\pm4_{}`

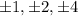
The factors of the Leading coefficient are

`\pm1,\pm3`

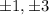
The root of the p(x) are

`\begin{gathered} (p)/(q) \\ \text{where p=factors of the constant term } \\ q=\text{factor of leading coefficient } \end{gathered}`

hence , the possible root of p(x) are

`\pm1,\pm(1)/(3),\pm2,\pm(2)/(3),\pm4,\pm(4)/(3)`

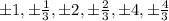
Hence

root of p(x) are 2/3, -2, and 1