Question

Find the acute angle between the lines 2y+x=1 and x+3y=6

Answer 1

Given the equations of the lines:

`\begin{gathered} 2y+x=1 \\ x+3y=6 \end{gathered}`

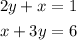
the given equations written in standard form, we will rewrite in in the slope-intercept form

So,

`\begin{gathered} y=-(1)/(2)x+(1)/(2) \\ y=-(1)/(3)x+(6)/(3) \end{gathered}`

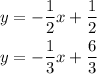
So, the slopes of the lines are { -1/2, -1/3 }

The acute angle between the lines of slopes m1 and m2 is given by the formula:

`\text{tan}\theta=|\frac{m_{1_{}}-m_2}{1+m_1m_2}|`

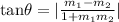
Substitute with slopes of the lines

So,

`\tan \theta=|(-(1)/(2)-(-(1)/(3)))/(1+(-(1)/(2))(-(1)/(3)))|=|(-(1)/(6))/(1+(1)/(6))|=(1)/(7)`

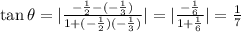
so, the angle will be:

`\theta=\tan ^(-1)((1)/(7))=8.13\degree`

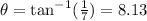
So, the answer will be the acute angle = 8.13°