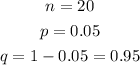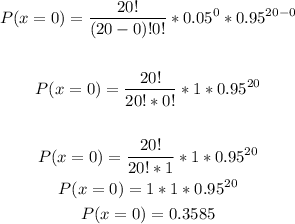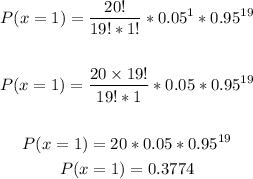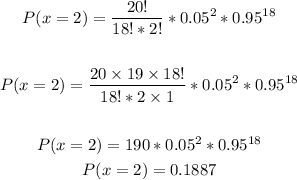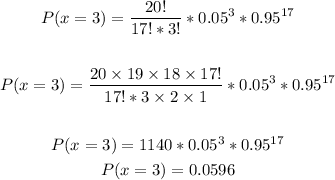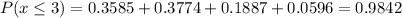Binomial distribution formula:
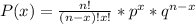
________
n = 15, p = 0.4, find P(4 successes)
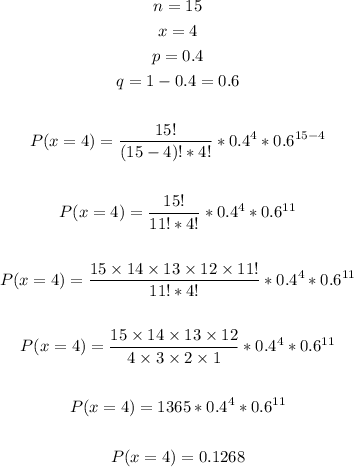
__________________
n = 12, p = 0.2, find P(2 success )
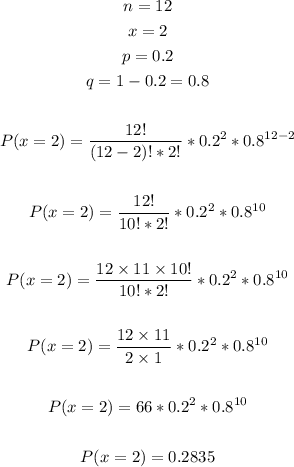
_________________________
n = 20, p = 0.05, find P(at most 3 successes)
Find each part (P(x=0), P(x=1), P(x=2), P(x=3)) and then sum the results