Let's draw a diagram of the situation:
According to the information of the problem, we have 760 feet of fencing available, which means
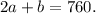
The area of this enclosure would be
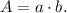
Let's rewrite the equation of the perimeter we got earlier to make one of the variables depend on the other:
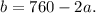
Now let's use this value of b in the formula for the area:
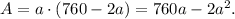
We can consider this as a function of a:
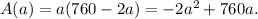
From
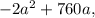
we can tell that the function is a parabola.
From
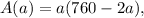
we can tell that A(a)=0 when a=0 and when a=380. Since the leading term of the parabola is negative (-2) this means that we can think of the parabola starting at (0,0) going up, reaching a certain maximum and then going down to reach (0,380):
Since a parabola is simmetrical, we can conclude that it will reach its highest point at the midpoint between 0 and 380. In other words, it will reach its maximum when a=190.
And when a=190:
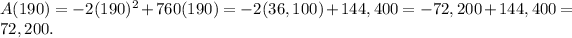
Thus, the maximum possible are of the enclosement is 72,200 square feet.