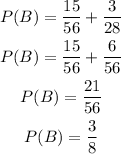Probabilities
We have the following elements to choose from:
Rock songs (R) = 2
Reggaes songs (G) = 3
Country songs (C) = 3
It's required to find two probabilities:
a) The first is a rock song
As stated above, there are R = 2 rocks songs and there are 8 songs in total, thus the probability of randomly picking a rock song is:
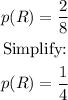
b) The second song is a country song.
This is quite more complex to calculate. Let's assume the first song was not a Country song (NC). This has a probability of:
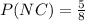
Since there are 5 non-country songs out of 8. For the second pick, we have all of the country songs unplayed out of 7, thus the probability of selecting it is:
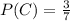
The probability of this 'brank' of events is:
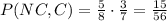
Now assume the first song was actually a country song. It has a probability of:
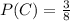
For the second pick, we now have only 2 country songs out of 7, so the probability of selecting another country song is:
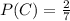
The probability of this 'branch' of events is:
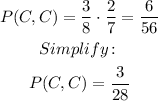
The total probability of selecting a country song as the second song is: