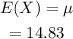Question

Consider the discrete random variable X giving in the table below calculate the mean variance and standard deviation of X also calculate the expected value of X round solution to 3 decimal places

Answer 1

Given data:

First we will find :

`x\mathrm{}p(x)andx^2p(x)`

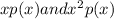
X P(x) x.p(x) x^2.p(x)

4 0.13 0.52 2.08

8 0.08 0.64 5.12

11 0.13 1.43 15.73

12 0.12 1.44 17.28

20 0.54 10.8 216

total 14.83 256.21

For x.p(x), we will multiply x and p(x).

Similarly, x^2.p(x) we will multiply x twice and p(x).

Now,

(a) mean is given as:

Hence, from the calculation above, we have:

`\text{Mean}=14.83`

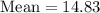
(b) Variance is given by:

`\begin{gathered} \text{Variance(}\sigma^2)=\Sigma.x^2p(x)^{}-\mu^2 \\ =256.21-219.9289 \\ =36.2811 \\ \approx36.281 \end{gathered}`

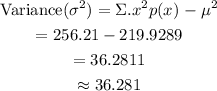
(c) Standard deviation is given by:

`\begin{gathered} \text{Standard deviation(}\sigma)=\sqrt[]{36.2811} \\ =6.02337 \\ \approx6.023 \end{gathered}`

(d) Expectation value of X is given by:

`\begin{gathered} E(X)=\mu \\ =14.83 \end{gathered}`