Question

A cone with a radius of 15cm and a height of 10cm is filled with water. The cone is then poured into a 3D rectangular solid with dimensions 14cm by 17cm by 25cm. How many full cones can be poured into the rectangular solid without it overflowing

Answer 1

The volume of cone =

`\text{Volume}_(cone)\text{ = }(1)/(3)\pi\text{ r}^2\text{ h}`

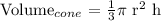
where r = 15cm

h = 10 cm

PI = 3.14

V= 1/3 x 3.14 x 15 x 15 x 10

V = 2355/3

`V=785cm^3`

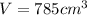
Also, let us consider the volume of the rectangular solid

The volume of the rectangular solid = L X B X H

L= 14cm, B = 17cm , H = 25cm

V = 14 x 17 x 25

`V=5950cm^3`

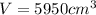
To determine the number of full cones of water that will be obtained in the rectangular solid, we will divide the volume of the rectangular solid by that of the cone

`\begin{gathered} (5950)/(785) \\ \\ \Rightarrow\text{ 7.58} \end{gathered}`

Since the water shouldn't overflow, we will round up to the nearest whole number

=> 8