Given the points on the line:
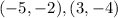
You can find the slope of the line using this formula:

Where these two points are on the line:

In this case, you can set up that:
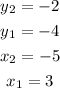
Then, substituting values into the formula and evaluating, you get:

• By definition, the Point-Slope Form of the equation of a line is:
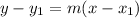
Where "m" is the slope and this is a point on the line:
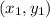
In this case, having the two points on the line shown in the exercise, you can substitute their coordinates into the equation and simplify, in order to get two equations for the line in Point-Slope Form:
- Using the point:
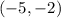
You get:
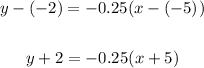
- Using the point:
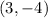
You get:
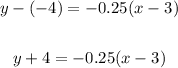
• By definition the Slope-Intercept Form of the equation of a line is:
![undefined]()