The given equations are:
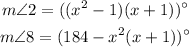
Notice from the figure that angles 2 and 6 are corresponding angles, hence, they must have equal measures. It follows that:
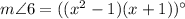
Notice from the figure that the angles 6 and 8 form a linear pair, hence, they must be supplementary, that is, the sum of their measures must be 180º:
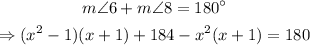
 The value of x is 3.
The value of x is 3.