Question

I have question about a part of a math problem involving removing complex numbers from an demoninator.The part of the problem in question is this:-5i/2i^2 + 1/2 = -5i/2*(-1) +1/2Why does the denominator go from 2i^2 to 2*(-1) on the denominator?

Answer 1

So you have this expression:

`-(5i)/(2i^2)+(1)/(2)`

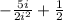
And it is simplified to this:

`-(5i)/(2i^2)+(1)/(2)=-\frac{5i}{2\cdot(-1)^{}}+(1)/(2)`

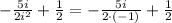
The property used in this simplification comes from the definition of the imaginary number i. Let's recall that i is defined as:

`i=\sqrt[]{-1}`

Then if we square both sides of this equation we get:

`\begin{gathered} i^2=(\sqrt[]{-1})^2 \\ i^2=-1 \end{gathered}`

And that is the reason behind the simplification performed.