Question

Lesson: 1.08Given this function: f(x) = 4 cos(TTX) + 1Find the following and be sure to show work for period, maximum, and minimum:Period =Equation of the mideline:Maximum =Minimum =

Answer 1

The given function is

`f(x)=4\cos \text{(}\pi x)+1`

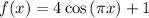
The general form of the cosine function is

`y=a\cos (bx+c)+d`

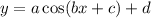
a is the amplitude

2pi/b is the period

c is the phase shift

d is the vertical shift

By comparing the two functions

a = 4

b = pi

c = 0

d = 1

Then its period is

`\begin{gathered} \text{Period}=(2\pi)/(\pi) \\ \text{Period}=2 \end{gathered}`

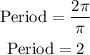
The equation of the midline is

`y_(ml)=(y_(\max )+y_(\min ))/(2)`

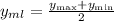
Since the maximum is at the greatest value of cos, which is 1, then

`\begin{gathered} y_(\max )=4(1)+1 \\ y_(\max )=5 \end{gathered}`

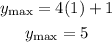
Since the minimum is at the smallest value of cos, which is -1, then

`\begin{gathered} y_(\min )=4(-1)+1 \\ y_(\min )=-4+1 \\ y_(\min )=-3 \end{gathered}`

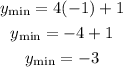
Then substitute them in the equation of the midline

`\begin{gathered} y_(ml)=(5+(-3))/(2) \\ y_(ml)=(2)/(2) \\ y_(ml)=1 \end{gathered}`

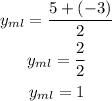
The answers are:

Period = 2

Equation of the midline is y = 1

Maximum = 5

Minimum = -3