The given equation is-
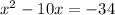
First, we move the independent term to the other side.
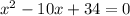
Now, we have to use the quadratic equation to find the solutions.-
![x_(1,2)=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/li72dimqx1poek8bdg3bs589861h83kfxl.png)
Where, a = 1, b = -10, and c = 34.
Replacing these values in the formula, we have.
![\begin{gathered} x_(1,2)=\frac{-(-10)\pm\sqrt[]{(-10)^2-4(1)(34)}}{2(1)} \\ x_(1,2)=\frac{10\pm\sqrt[]{100-136}}{2}=\frac{10\pm\sqrt[]{-36}}{2} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/a2jwmbyndjfptv0rukerw9innhdzys3ss9.png)
But, there's no square root of -36 because it's a negative. To solve this issue, we use complex numbers that way, we would have solutions.
![x_(1,2)=\frac{10\pm\sqrt[]{36}i}{2}=(10\pm6i)/(2)=5\pm3i](https://img.qammunity.org/2023/formulas/mathematics/high-school/jbi2olcu3wopzrda6wgrp0upu6y8k2zrbl.png)
Therefore, the solutions are
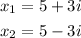
The right answer is B.