Answer:
93.5 units
Step-by-step explanation:
The function that models the approximate height is given as:
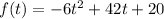
To determine how high the object goes, we find the maximum height ( or vertex) of the parabola.
First, find the equation of the line of symmetry using the formula below:
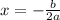
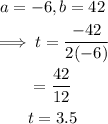
Next, substitute t=3.5 into f(t) to find the maximum height.
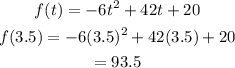
The object goes as high as 93.5 units.
To demonstrate, the graph is attached here:
We see that the graph goes as high as 93.5 units (which was our result).