Question

a simple pendulum has a period of 2.0s. What is the new period of the pendulum if its length is doubled?

Answer 1

Take into account that the period of a pendulum is given by the following expression:

`T=2\pi\sqrt[]{(l)/(g)}`

where l is the length of the pendulum and g the acceleration gravitational constant (9.8m/s^2).

In order to determine the new period of the pendulum, first solve the equation above for l, as follow:

`l=(gT^2)/(4\pi^2)`

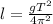
When the priod is T=2.0s, the length l is:

`l=((9.8(m)/(s^2))(2.0s)^2)/(4\pi^2)\approx1.0m`

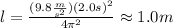
Then, if the length is doubled, that is, if l=2.0m, the new period is:

`T=2\pi\sqrt[]{(2.0m)/(9.8(m)/(s^2))}\approx0.45s`

Hence, the new period of the pendulum is approximately 0.45s