Question

use an appropriate local linear approximation to estimate the value of the given quantity.answer q3 only.

Answer 1

In this case, we know that

`cos30=\frac{\sqrt[\placeholder{⬚}]{3}}{2}`

so we can use this value to estimate cosine of 32 degrees.

The local linear approximation is given by

`y-y_1=m\lparen x-x_1)`

where, in our case,

`\begin{gathered} x=32 \\ x_1=30 \\ y=cos32 \\ y_1=cos30=(√(3))/(2) \end{gathered}`

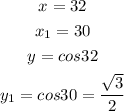
and m is the derivative of the function

`cos\theta`

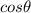
evaluated at

`\theta=30\text{ degrees}`

In this regard, the derivative of cosine of thetat is given by

`(d)/(d\theta)cos\theta=-sin\theta`

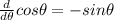
then the slope m is given as

`m=(d)/(d\theta)cos\theta_(\theta=30)=-s\imaginaryI n30=-(1)/(2)`

Then by substituting this value and the above ones on the local linear approximation, we have

which gives

`\begin{gathered} cos32-(√(3))/(2)=-(1)/(2)\left(2\right) \\ cos32-(√(3))/(2)=-1 \end{gathered}`

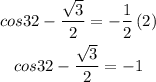
then by moving square root of 3 over 2 to the right hand side, we get

`cos32=-1+\frac{\sqrt[\placeholder{⬚}]{3}}{2}`