Question

2Let be an angle such that tan 6 = and cos 0 <0.7Find the exact values of seco and csco.1 2 3 4

Answer 1

`\begin{gathered} \sec \theta=\frac{\sqrt[]{53}}{7} \\ \csc \theta=\frac{\sqrt[]{53}}{2} \end{gathered}`

Step-by-step explanation

The trigonometric function tangent is defined as follows:

`\tan \theta=\frac{\text{opposite}}{\text{adjacent}}`

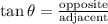
Where

"opposite" refers to the side across the angle θ in the right triangle

"adjacent" refers to the side next to the angle θ in the right triangle

The secant is the reciprocal function of the cosine:

`\sec \theta=(1)/(\cos \theta)=\frac{\text{hypotenuse}}{\text{adjacent}}`

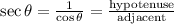
The cosecant is the reciprocal function of the sine:

`\csc \theta=(1)/(\sin \theta)=\frac{\text{hypotenuse}}{\text{opposite}}`

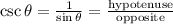
To calculate the cosecant and secant, the first step is to determine the length of the hypothenuse of the triangle.

Considering the given tangent:

`\tan \theta=\frac{\text{opposite}}{\text{adjacent}}=(2)/(7)`

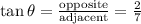
We know that the legs of the triangle have a measure 2units and 7units, using the Pythagorean theorem, we can calculate the length of the hypothenuse:

`a^2+b^2=c^2`
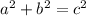
`\begin{gathered} 2^2+7^2=c^2 \\ 4+49=c^2 \\ 53=c^2 \\ \sqrt[]{53}=\sqrt[]{c^2} \\ \sqrt[]{53}=c \end{gathered}`

So,

Opposite=2

Adjacent=7

Hypotenuse =√53

Secant:

`\begin{gathered} \text{sec}\theta=(hypotenuse)/(adjacent) \\ \sec \theta=\frac{\sqrt[]{53}}{7} \end{gathered}`

Cosecant:

`\begin{gathered} \csc \theta=\frac{\text{hypotenuse}}{\text{opposite}} \\ \csc \theta=\frac{\sqrt[]{53}}{2} \end{gathered}`