Question

Graph the following system of inequalities on the coordinate plane. You will need to explain your work. Each correct line graphed WITH the correct explanation and shading is worth 2 points.

Answer 1

for y > - 3x - 2

how did you graph the line?

You would draw the line y = - 3x - 2

how did you determine where to shade?

1. We shade above (not below) because y is greater than the other side of the inequality.

2. We draw a dashed line (not solid) because we aren't dealing with an "or equal to" inequality. The dashed line indicates that points on the line are not solutions to the inequality.

The graph:

for 4x + 5y <= 20

how did you graph the line?

1. We put it in slope-intercept form:

`\begin{gathered} 4x+5y\leq20 \\ 4x+5y-4x\le20-4x \\ 5y\le20-4x \\ (5y)/(5)\le(20)/(5)-(4x)/(5) \\ y\le-(4)/(5)x+4 \end{gathered}`

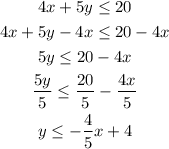
2. You would draw the line

`y=-(4)/(5)x+4`

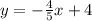
how did you determine where to shade?

1. We shade below (not above) because y is less than (or equal to) the other side of the inequality.

2. We draw a solid line (not dashed) because we're dealing with an "or equal to" inequality. The solid line indicates that points on the line are solutions to the inequality.

The graph is:

for y > - 4

how did you graph the line?

You would draw the line y = - 4

how did you determine where to shade?

1. The graph is shaded above (not below), so y is greater than the other side of the inequality.

2. The graph has a dashed line (not solid), so we aren't dealing with an "or equal to" inequality.

The graph is: