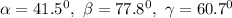Question

Solve the triangle a=6.3 b=9.3 c=8.3 if it is not possible say so

Answer 1

Step 1:

First, we need to determine if the triangle is solvable or not by applying the triangle inequality theorem which states that the sum of any two sides of a triangle must be greater than the measure of the third side

In our case,

`\begin{gathered} a+b>c \\ a+c>b \\ b+c>a \end{gathered}`

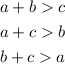
Therefore, the triangle is solvable

Step 2:

The given sides of the triangle are a = 6.3, b = 9.3, c =8.3

We need to find the three angles of the triangles labelled above. In order to do this, we need to apply the cosine rule,

To calculate the first angle α,

`\begin{gathered} \cos \alpha=(b^2+c^2-a^2)/(2bc) \\ \cos \alpha=(9.3^2+8.3^2-6.3^2)/(2*9.3*8.3) \\ \cos \alpha=\frac{86.49^{}+68.89^{}-36.69}{117.18} \\ \cos \alpha=\frac{115.69^{}}{154.38} \\ \cos \alpha=0.7494 \\ \alpha=41.5^0 \end{gathered}`

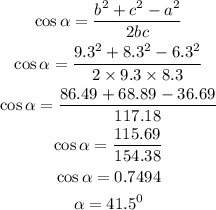
To calculate the second angle β

`\begin{gathered} \cos \beta=\frac{a^2+c^2-b^2^{}}{2ac} \\ \cos \beta=(6.3^2+8.3^2-9.3^2)/(2*6.3*8.3) \\ \cos \beta=\frac{39.69^{}+68.89^{}-86.49^{}}{2*6.3*8.3} \\ \cos \beta=\frac{22.09^{}}{104.58} \\ \cos \beta=0.2112 \\ \beta=\cos ^(-1)(0.2112) \\ \beta=77.8^0 \end{gathered}`

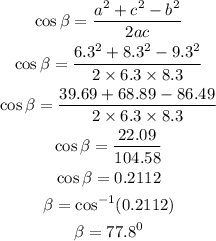
To calculate the third angle,

`\begin{gathered} \gamma=\text{ 180 - (41.5+77.8})\text{ (sum of angles in a triangle is 180deg.)} \\ \gamma=60.7^0 \end{gathered}`

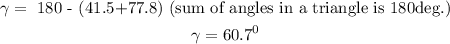
Therefore, the measures of the angles of the triangle are:

`\alpha=41.5^0,\text{ }\beta=77.8^0,\text{ }\gamma=60.7^0`